
今日の板書はこれ!
\(y=f(x)\) を \(x\) 軸、\(y\) 軸、原点に関して対称移動した関数 \(y=g(x)\)
- \(x\) 軸対称:\(-y=f(x)\)
- \(y\) 軸対称:\(y=f(-x)\)
- 原点対称:\(-y=f(-x)\)

もっと詳しく願いします!!
こんにちは、現役教員の「さん」です。
「人より勉強に時間がかかる…」と悩んでいませんか?
私の学校でも、教科書の説明が難しくて止まってしまう生徒がたくさんいます。
• 「\(x\) 軸対称なのに、\(y\) にマイナスをつけるのはなぜ?」
• 「原点対称って、結局どうすればいいの?」
数学を理解するコツは、「自分なりに噛み砕いて考えること」。
今回は、平行移動のときと同じ「最強の考え方」を使って、対称移動をマスターしましょう!
2次関数のグラフの対称移動
対称移動の考え方:やっぱり「逆転の発想」
対称移動も、考え方は平行移動と全く同じ。
「移動後の点 \((x,y)\) を、元の位置に逆戻りさせて、元のルール(式)に当てはめる」だけです
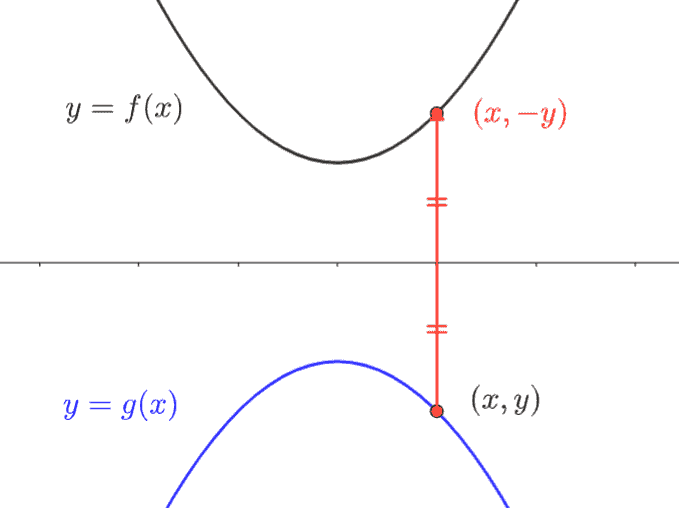
x軸対称(上下パタン!)
移動後の点 \((x,y)\) を \(x\) 軸で折り返して元に戻すと、点は \((x, -y)\) になります。
これを元の式に代入する、つまり \(y=f(x)\) の \(y\) を \(-y\) に置き換えます。
\(-y=f(x)\)
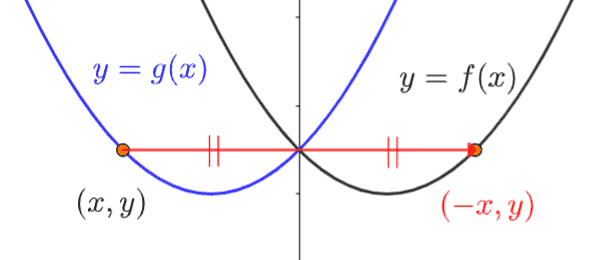
y軸対称(左右パタン!)
移動後の点 \((x,y)\) を \(y\) 軸で折り返して元に戻すと、点は \((-x, y)\) になります。
これを元の式に代入する、つまり \(y=f(x)\) の \(x\) を \(-x\) に置き換えます。
\(y=f(-x)\)
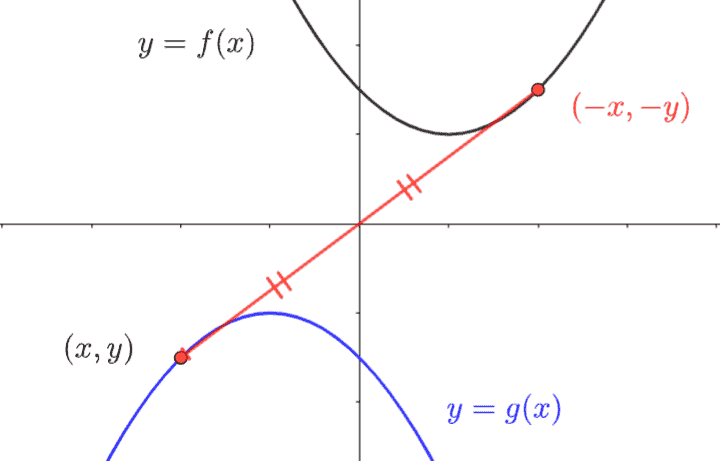
原点対称(くるっと180度!)
移動後の点 \((x,y)\) を原点を中心に元に戻すと、点は \((-x, -y)\) になります。
これを元の式に代入する、つまり \(y=f(x)\) の \(x\) を \(-x\) に、\(y\) を \(-y\) に置き換えます。
\(-y=f(-x)\)
例題で計算のコツを掴もう!

例題で、知識を定着させよう!
2次関数\(y=x^2-2x+3\) のグラフの、\(x\) 軸、\(y\) 軸、原点それぞれに関する対称移動後の放物線の方程式を求めよ。
x軸対称
\(y\) を \(-y\) に入れ替えます。
\(\color{red}{-y}=x^2-2x+3\) より \(y=-x^2+2x-3\)
y軸対称
\(x\) を \((-x)\) に入れ替えます。
\(y=\color{red}{(-x)}^2-2\color{red}{(-x)}+3\) より \(y=x^2+2x+3\)
原点対称
\(x\) を \((-x)\) に、\(y\) を \(-y\) に入れ替えます。
\(\color{red}{-y}=\color{red}{(-x)}^2-2\color{red}{(-x)}+3\) より \(y=-x^2-2x-3\)

「逆に移動させて元に戻す」と考えれば、どの座標の符号を変えればいいか迷わなくなりました!

その通り!「\(x\) 軸対称は \(y\) を変える」みたいに、あべこべになる感覚もこれで納得だね。
まとめ:2次関数のグラフの対称移動

さて、今回のまとめだよ!
\(y=f(x)\) を \(x\) 軸、\(y\) 軸、原点に関して対称移動した関数 \(y=g(x)\)
- \(x\) 軸対称:\(-y=f(x)\)
- \(y\) 軸対称:\(y=f(-x)\)
- 原点対称:\(-y=f(-x)\)

ありがとうございました!!






コメント