
さん
今日の板書はこれ!
2次関数の最大・最小
- 平方完成をして、頂点を求める。
- グラフを描く。(「上に凸」か「下に凸」か注意!)
- 定義域(\(x\) の範囲)をグラフに描き込み、一番高い所と低い所を探す。

生徒
もっと詳しく願いします!!
こんにちは、現役教員の「さん」です。
「人より勉強に時間がかかる…」と悩んでいませんか?
私の学校でも、教科書の説明が難しくて止まってしまう生徒がたくさんいます。
• 「どこが最大で、どこが最小かパッと判断できない」
• 「『最大値なし』っていつ書けばいいの?」
数学を理解するコツは、「自分なりに噛み砕いて考えること」。
今回は、2次関数の最大・最小を「目で見ればわかる」ように解説していきます!
2次関数の最大・最小
最大・最小を求める「最強の3ステップ」
2次関数の最大・最小問題は、計算だけで解こうとせず、必ず次のステップを踏みましょう。
- 平方完成をして、頂点を求める。
- グラフを描く。(「上に凸」か「下に凸」か注意!)
- 定義域(\(x\) の範囲)をグラフに描き込み、一番高い所と低い所を探す。
パターン別・例題にチャレンジ!
例題
次の関数の最大値・最小値を求めよ。
(1) \(y=x^2-4x+3\)
(2) \(y=x^2-4+1 \:\:(0≦x≦3)\)
(3) \(y=-2x^2+4x+5 \:\:(-1≦x≦0)\)
(1) 範囲(定義域)がない場合
まずは平方完成です。
\(y=x^2-4x+3=(x-2)^2-1\)
グラフを描くと、
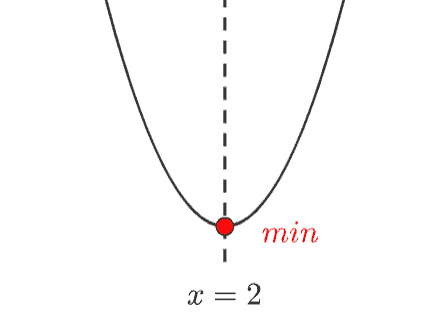
グラフより、
- 最大値なし(グラフはどこまでも上に伸びていく)
- \(x=2\) のとき最小値 \(-1\)(頂点の \(y\) 座標)

生徒
最大値が存在しないときは、ハッキリ「なし」って答えるのがルールなんだね!
(2) 範囲(定義域)がある場合
平方完成すると、\(y=x^2-4+1=(x-2)^2-3\)
グラフと定義域を描くと、
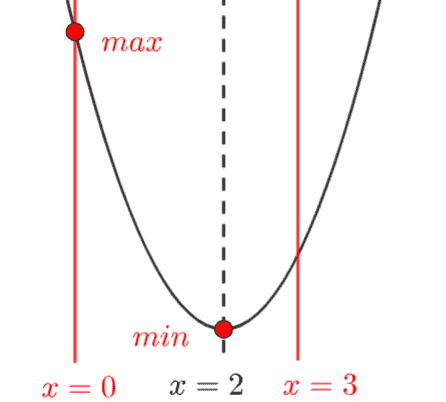
グラフより、
- \(x=0\) のとき最大値 \(1\)
- \(x=2\) のとき最小値 \(-1\)

さん
\(x=0\) のときの \(y\) の値は、平方完成した後の式より、元の式\(y=x^2-4+1\) に代入した方が計算ミスがなくて楽だよ!

生徒
グラフや定義域を描くと最大・最小が目で見てわかるね!
(3) 頂点が範囲の外にある場合
平方完成すると、\(y=-2x^2+4x+5=2(x-1)^2+7\)
グラフを描くと、
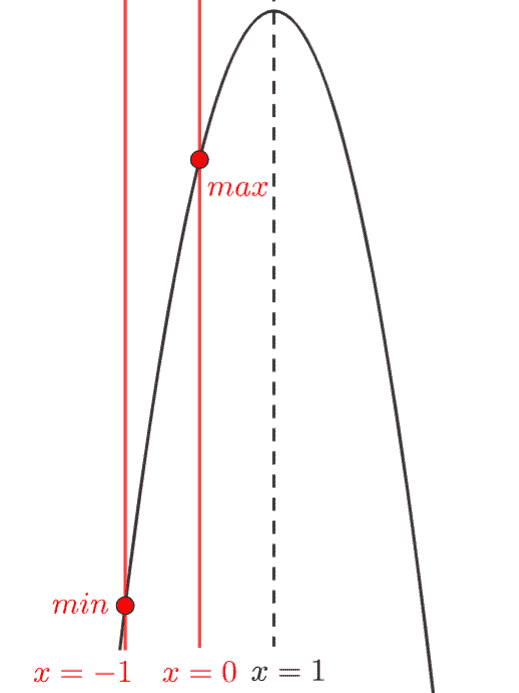
グラフより、
- \(x=0\) のとき最大値 \(5\)
- \(x=-1\) のとき最小値 \(-1\)

さん
もし定義域が \(-1<x≦0\) (\(x=-1\) を含まない)だったら、「最小値なし」という答えになるから注意してね!
まとめ:2次関数の最大・最小

さん
さて、今回のまとめだよ!
2次関数の最大・最小
- 平方完成をして、頂点を求める。
- グラフを描く。(「上に凸」か「下に凸」か注意!)
- 定義域(\(x\) の範囲)をグラフに描き込み、一番高い所と低い所を探す。

生徒
ありがとうございました!!






コメント