【数学Ⅰ】2次関数08：2次関数の最大・最小から係数決定

---

---

こんにちは、現役教員の「さん」です。

「問題に文字（\(c\)など）が混じると、急に難しく感じる…」と悩んでいませんか？

今回のテーマは、「係数決定」。

答え（最大値など）が先にわかっている状態で、式の「穴あき」部分を埋める問題です。

数学を理解するコツは、「自分なりに噛み砕いて考えること」。

実はこれ、これまでの「最大・最小」の知識があれば、パズルを解くように簡単に攻略できるんですよ！

2次関数の最大・最小から係数決定

例題で「逆算のテクニック」を学ぼう！

与えられた情報は「最大値が \(8\) 」から、関数の係数 \(c\) を求める問題です。

係数決定の攻略法：まずは「いつも通り」でOK！

文字 \(c\) が入っていても、やることは変わりません。

「文字 \(c\) を持ったまま、いつも通りにグラフを描く」のが最大のポイントです。

1. 平方完成をする（ \(c\) はそのまま残しておく）。
2. グラフを描き、最大・最小をとる場所を特定する。
3. その場所の値を計算し、問題文の数字とイコールで結ぶ（方程式を作る）。

STEP 1：文字 c を含んだまま「平方完成」

\(y=x^2-4x+c=(x-2)^2+c-4\)

これより、頂点は \((2, c – 4)\) だとわかります。

STEP 2：グラフを描いて「最大値」の場所を探す

軸は \(x = 2\) です。

定義域 \(1≦x≦5\) を描き込んでみましょう。

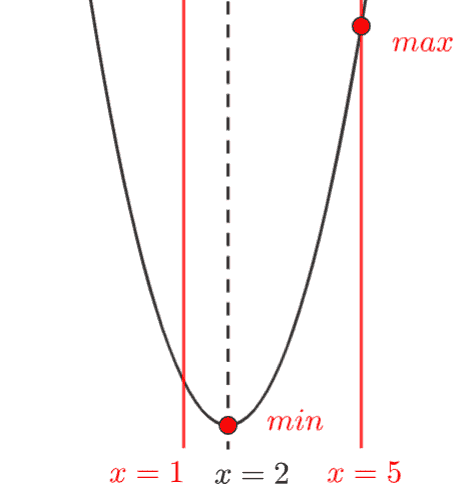
グラフを見ると、軸（\(x=2\)）からより遠い \(x=5\) のときが最大値になることが一目でわかりますね！

STEP 3：方程式を作って c を決定する

\(x=5\) のときの \(y\) の値を計算します。

\(y=(5-2)^2+c-4=c+5\)

この「\(c + 5\)」が、問題文にある最大値「\(8\)」になればいいので……

\(c+5=8\)

これを解いて、 \(c=3\) ！！

まとめ：2次関数の最大・最小から係数決定

---

---